Next: 線形システムのボードとナイキスト周波数応答 Up: 例題 Previous: 離散系リカッティ方程式

線形システムの伝達関数行列

線形システム

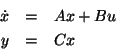
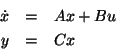
$\begin{displaymath}\begin{array}{rcl} \dot{x} & = & A x + B u \\ y & = & C x \end{array}\end{displaymath}$

の伝達関数行列

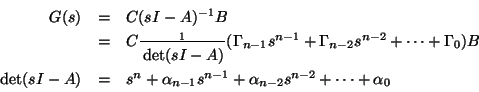
$\begin{displaymath}\begin{array}{rcl} G(s) & = & C (s I - A)^{-1} B \\ & = & C... ...}s^{n-1} + \alpha_{n-2}s^{n-2} + \cdots + \alpha_0 \end{array}\end{displaymath}$

をファディーブのアルゴリズムにより求める。ファディーブのアルゴリズムにより $\Gamma_i$ と $\alpha_i$ は，

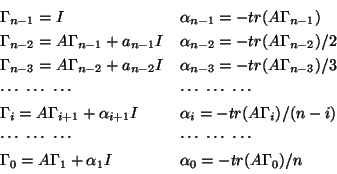
$\begin{displaymath}\begin{array}{ll} \Gamma_{n-1} = I & \alpha_{n-1} = - {\rm t... ...1 + \alpha_1 I & \alpha_0 = - {\rm tr}(A\Gamma_0)/n \end{array}\end{displaymath}$

と与えられる。ただし， ${\rm tr}(X)$ は，行列Xの対角成分の和を意味する。

   Func void main()
   {
     Matrix A, B, C, G;    // 変数の宣言
     Matrix Faddeev();
05:
     read A, B, C;         // 行列の読み込み
     G = Faddeev(A, B, C); // Faddeev()を呼ぶ
     print G;              // G を表示
   }
10:
   Func Matrix Faddeev(A, B, C)
     Matrix A, B, C;
   {
     Matrix Gamma, N;
15:  Polynomial s, ch;
     Integer i, n;
   
     s = $;            // 多項式の変数
     n = Rows(A);      // システムの次数
20:
     Gamma = Z(n,A);
     ch = Polynomial(Z(1,n+1)); 
                       // 特性多項式
     ch(n) = 1.0;      // 最高次の係数は 1
25:
     Gamma(n-1,A) = I(n);
     ch(n-1) = - trace(A);
   
     for (i = n-2; i >= 0; i--) {
30:      Gamma(i,A) = A*Gamma(i+1,A) + ch(i+1)*I(n);
         ch(i) = - trace(A*Gamma(i,A))/(n - i);
     }
   
     N = Z(Rows(C), Cols(B));   
35:  for (i = 0; i < n; i++) {
         N = N + C*Gamma(i,A)*B * s^i;
     }
   
     return N/ch;      // 伝達関数を返す
40:}

List 3: ファディーブのアルゴリズムによる伝達関数の計算

Masanobu KOGA 平成10年8月19日