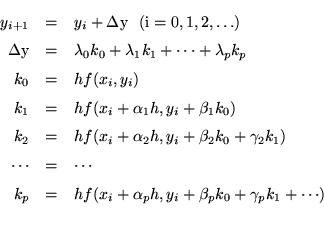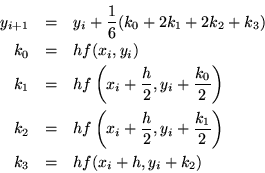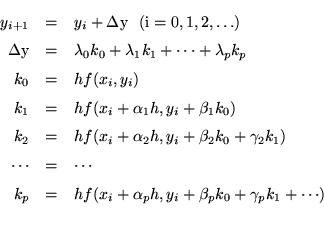
Matrix rngkut4(Real t, Matrix x, Matrix dx(),
Matrix u, Real dt)
t: 時間
x: 状態
dx(): dxを返す関数
u: 入力
dt: きざみ時間
dtが省略された時にはdt = 1.0E-7が使われ,uが省略
された時には,u = Z(0)が使われます。
これはforループなどに用いることが出来ます。以下に例を示します。
Func void main()
{
Integer i, ii;
Real dt, t, t1, t2;
Matrix x, u;
Array X, U;
Matrix plant(), controller();
t1 = 0.0; // 初期時間
t2 = 5.0; // 終端時間
dt = 0.01; // 刻み時間
ii = Integer((t2 - t1) / dt);
x = [1 1 1]'; // 初期状態
u = [0];
X = Z(1, ii, x);
U = Z(1, ii, u);
t = t1;
X(1, 1, x) = x;
for (i = 1; i < ii; i++) {
u = controller(t, x);
x = rngkut4(t, x, plant, u, dt);
U(1, i, u) = u;
X(1, i+i, x) = x;
t = t + dt;
}
print [[X][U]] >> "cont.mat";
}
Func Matrix plant(t, x, u)
Real t;
Matrix x, u;
{
Matrix dx, A, b;
A = [[ 0, 1, 0]
[ 0, 0, 1]
[-2, -3, -4]];
b = [0 0 1]';
dx = A * x + b * u;
return dx;
}
Func Matrix controller(t, x)
Real t;
Matrix x;
{
Matrix f, u;
f = [ -1, -1, -1];
u = f * x;
return u;
}
このプログラムはシミュレーションの基礎となるプログラムです。
Ode()とはかなり形式が異なるので注意して下さい。Ode()はdx
を返す関数と,uを返す関数を作って,それをOde()の引数に書
けば,積分をやってその結果も書き出してくれますが,このrngkut4()
は純粋にルンゲクッタ法をやってくれるだけなので,このようにfor
で書く必要があります。ルンゲクッタ法の具体的なアルゴリズムは次のよ
うになります。
y' = f(x,y)という関数が存在し,
(xi, yi)から yi+1を求め
るステップが次のようなアルゴリズムで示されているとき,p+1次のルン
ゲクッタ法であると言います。