



Next: 倒立振子の制御のシミュレーション
Up: リアルタイム処理(RTMATX)
Previous: リアルタイム処理用関数
ここでは,図D.1に示す倒立振子のオブザーバ+状態フィード
バックによる制御について,シミュレーションおよびリアルタイム制御の
プログラムの例を示す。
台車についての運動方程式は
である。ただし
| M | [kg] |
: | 台車・プーリ・モータ系の等価質量 |
| r | [m] |
: | 台車の変位 |
| u | [V] |
: | パワーアンプへの入力電圧 |
| a | [N/V] |
: | uから台車に働く力までのゲイン |
| F | [N/(m/s)] |
: | 台車・ベルト・プーリ・モータ系の等価摩擦係数 |
| H | [N] |
: | 振子から台車に働く水平力 |
である。ただし,
| J | [kgm2] |
: | 振子の重心回りの慣性モーメント |
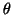 | [rad] |
: | 振子の鉛直線下からの角度 |
| V | [N] |
: | 台車から受ける力の垂直方向成分 |
| l | [m] |
: | 軸から振子の重心までの距離 |
| H | [N] |
: | 台車から受ける力の水平方向成分 |
| c | [kgm2/s] |
: | 軸の摩擦係数 |
| m | [kg] |
: | 振子の質量 |
| g | [m/s2] |
: | 重力加速度 |
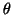 ,台車の速度
,台車の速度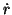 ,
振子の角速度
,
振子の角速度
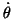 をとり,状態ベクトルを
をとり,状態ベクトルを
とすると,倒立振子の状態方程式は次のように書ける。
ここで,
ただし,
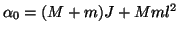 である。
である。
平衡点近傍で線形近似を行なって得た線形モデルに対して,
オブザーバと状態フィードバック則を設計して,シミュレーションおよび
リアルタイム制御(実験)を行なう。




Next: 倒立振子の制御のシミュレーション
Up: リアルタイム処理(RTMATX)
Previous: リアルタイム処理用関数
Masanobu KOGA
平成10年8月19日
![\includegraphics[width=0.5\linewidth]{Fig/pendulum.eps}](img64.gif)
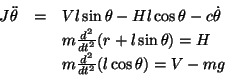
![\begin{displaymath}x = \left[\begin{array}{c}
x_1\\ x_2\\ x_3\\ x_4
\end{array}...
...ray}{c}
r\\ \theta\\ \dot{r}\\ \dot{\theta}
\end{array}\right]
\end{displaymath}](img70.gif)
![\begin{displaymath}\begin{array}{rcl}
\dot{x} = f(x, u) \df &&
\left[
\begin{...
...cos x_2 x_4^2 + b_4 \cos x_2 u\}
\end{array}\right]
\end{array}\end{displaymath}](img71.gif)
![\begin{displaymath}\left[
\begin{array}{ccccc}
a_{32} & a_{33} & a_{34} & a_{35...
...a_{43} & a_{44} & a_{45} & b_4
\end{array}\right]\hspace*{4cm}
\end{displaymath}](img73.gif)